

|
||||
|
|
Journal of Neuroscience Methods
Volume 167, Issue 1, 15 January 2008, Pages 105-114 Brain-Computer Interfaces (BCIs) |
| ||||
|
| |||||||||||||||||||||
|
Prediction of arm movement trajectories from ECoG-recordings in humans
Tobias Pistohla, b, c,  ,
,  , Tonio Balla, c, d, Andreas Schulze-Bonhagea, d, Ad Aertsena, c and Carsten Mehringa, b
, Tonio Balla, c, d, Andreas Schulze-Bonhagea, d, Ad Aertsena, c and Carsten Mehringa, b
aBernstein Center for Computational Neuroscience, Albert-Ludwigs-University, Freiburg, Germany
bNeurobiology and Animal Physiology, Faculty of Biology I, Albert-Ludwigs-University, Freiburg, Germany
cNeurobiology and Biophysics, Faculty of Biology III, Albert-Ludwigs-University, Freiburg, Germany
dEpilepsy Center, University Clinics, Albert-Ludwigs-University, Freiburg, Germany
Received 16 April 2007; revised 16 September 2007; accepted
1 October 2007. Available online 10 October 2007.
Electrocorticographic (ECoG) signals have been shown to contain reliable information about the direction of arm movements and can be used for on-line cursor control. These findings indicate that the ECoG is a potential basis for a brain-machine interface (BMI) for application in paralyzed patients. However, previous approaches to ECoG-BMIs were either based on classification of different movement patterns or on a voluntary modulation of spectral features. For a continuous multi-dimensional BMI control, the prediction of complete movement trajectories, as it has already been shown for spike data and local field potentials (LFPs), would be a desirable addition for the ECoG, too. Here, we examined ECoG signals from six subjects with subdurally implanted ECoG-electrodes during continuous two-dimensional arm movements between random target positions. Our results show that continuous trajectories of 2D hand position can be approximately predicted from the ECoG recorded from hand/arm motor cortex. This indicates that ECoG signals, related to body movements, can directly be transferred to equivalent controls of an external effector for continuous BMI control.
Keywords: Decoding; Brain-machine interfaces; Neuronal motor prostheses; Motor control; Electrocorticography
It is well established that spike signals recorded from the motor cortex provide information about parameters of arm movements, like position and velocity of the hand, force or target position (e.g. [Thach, 1978], [Georgopoulos et al., 1982] and [Moran and Schwartz, 1999]). More recent studies showed that neuronal population signals, like intracortical local field potentials (LFPs) or field potentials measured directly from the brain surface (ECoG), also provide substantial information about movements ([Pesaran et al., 2002], [Mehring et al., 2003], [Leuthardt et al., 2004], [Ball et al., 2004], [Mehring et al., 2004], [Rickert et al., 2005] and [Scherberger et al., 2005]).
As this kind of information can directly be used in devices that give people control by means of their brain signals, studies in the field of brain-machine interfacing (BMI) have extensively investigated the potential of single trial decoding of movement related brain activity. Invasive recording techniques with intracortical microelectrodes have mainly been used in animal experiments ([Serruya et al., 2002], [Taylor et al., 2002] and [Carmena et al., 2003]), in some cases also in human experiments ([Kennedy et al., 2004] and [Hochberg et al., 2006]). However, most studies on the application of BMIs in humans explored non-invasive approaches like EEG (e.g. [Birbaumer et al., 1999], [Wolpaw et al., 2000], [Guger et al., 2000] and [Blankertz et al., 2003]). Considerable progress has been made with EEG-based BMIs (e.g. Wolpaw and McFarland, 2004), but whether this approach will ultimately have the potential for fast and precise control of an external effector with many degrees of freedom is still an open question. For technical reasons other non-invasive recording techniques (functional MRI, MEG) are currently not suitable for continuous, real-life application.
An alternative approach to record brain activity for a BMI is the electrocorticogram (ECoG) ([Levine et al., 2000], [Leuthardt et al., 2004], [Ball et al., 2004], [Mehring et al., 2004] and [Leuthardt et al., 2006]). The ECoG is used in patients for pre-neurosurgical diagnostics and represents a class of semi-invasive, i.e. intracranial but not intracortical, recording techniques. Several reasons suggest that ECoG signals might be preferable in a BMI-application over spike data or LFP recordings:
• ECoG-electrodes do not penetrate the cortical surface, thereby reducing the potential risk for brain tissue damage.
• In contrast to spike data which reflect single cell activity, ECoG (and LFP) measure population activity, which offers a better prospect of long-term recording stability.
• ECoG (as LFP) requires lower sampling rates for recording and no spike detection and sorting, thus reducing computational costs.
• Pioneering investigations using the ECoG can already be done with patients with diagnostic implantations (as in epilepsy pre-surgical diagnostics), without additional risks for the patients.
ECoG signals have already proven suitable for the decoding of a limited set of discrete arm movements ([Levine et al., 2000], [Leuthardt et al., 2004], [Mehring et al., 2004] and [Ball et al., 2004]). Real-life applications, however, often have to work in a continuous space. For this purpose, recent EEG or ECoG approaches either attempted to transform decoding of discrete classes into graded output variables (e.g. Blankertz et al., 2006) or used the amplitudes of certain signal components (e.g. the spectral power in different frequency bands) as a continuous control signal (e.g. Leuthardt et al., 2006). The direct translation of continuous movements, inferred from neuronal signals, to a continuous control output, could enable a more natural and thus, more adequate control. Moreover, it might facilitate the subjects’ adaptation to a neuronal control task. The decoding of complete, continuous trajectories of natural movements would, therefore, make an important contribution, going beyond the mere classification of discrete tasks or states. Schalk et al. (2007) recently demonstrated that circular hand movement trajectories can be approximately inferred from ECoG signals. The aim of this study is to investigate movement trajectory prediction for less restricted, full two-dimensional target-directed movements, taking this approach one step further towards a useful application in brain-machine interfaces.
Six patients (see Table 1) suffering from intractable pharmaco-resistant epilepsy were included in the study after having given their informed consent. One patient was ambidextrous, all others right-handed, none showed clinical signs of pareses. The study was approved by the University Clinic's ethics committee.
Subject overview
Age Handedness Main Lesion Grid location S1 34 Right Suspected FCD left anterior insular cortex Left, frontal, some parietal and temporal contacts S2 57 Ambidextrous HS right; multiple contusion-related lesions of the left temporal frontal cortex Left. temporo-parietal, some frontal and occipital contacts S3 21 right FCD left precentral cortex Left, frontal, some parietal and temporal contacts S4 30 Right FCD right rolandic cortex Right, fronto-parietal, few temporal contacts S5 14 Right FCD right frontal cortex Right, frontal, few parietal and temporal contacts S6 27 Right FCD left supplementary motor area Left, fronto-parietal FCD: focal cortical dysplasia. HS: hippocampal sclerosis.
All subjects had stainless steel electrodes implanted, most of which were regular grids of 64 (8 × 8) or 48 (8 × 6) electrodes (4 mm electrode diameter with 10 mm inter-electrode distance). In some cases, additional linear electrode arrays and/or arrays with two rows of electrodes (same electrode size and spacing) were implanted. For the analysis, between 48 and 108 channels per subject were used in total. Electrodes were subdurally implanted above fronto-parieto-temporal regions of the left (subjects S1, S2, S3 and S6) or right (S4 and S5) hemisphere. The site of electrode implantation was exclusively based on the requirements of the clinical evaluation.
Electrocorticograms from the cortical hemisphere contralateral to the moving arm were recorded using a clinical AC EEG-System (IT-Med, Germany) at 256 Hz (subjects S1 and S5) or 1024 Hz (S2–S4 and S6) sampling rate and with a high-pass filter with 0.032 Hz cutoff frequency.
Electrical stimulation through the electrode grid was performed using an INOMED NS 60 stimulator (INOMED, Germany). Trains of 7 s duration consisted of 50 Hz pulses of alternating polarity square waves of 200 μs each. The intensity of stimulation was gradually increased up to 15 mA or to the induction of sensory and motor phenomena, whichever happened first. In this way, a functional mapping of the cortex, covered by the implanted electrodes, was possible (see Fig. 1 and Fig. 6).
Subjects were seated upright in a hospital bed. They moved the arm contralateral to the site of electrode implantation, controlling the movement of a green circular cursor on a vertical LCD screen at about 1.5 m distance. In subject S1 hand position was tracked using a computer mouse. For subjects S2–S5 hand position was tracked using a tracking device consisting of a vertical handle, grasped by the subjects, and a movement tracking system (Zebris Medical GmbH, Isny, Germany), which recorded the position of the handle. Movements were restricted to the horizontal plane. Subject S6 used a Joystick that translated inclination of the handle to cursor position. Subjects were instructed to guide the cursor onto a highlighted target, which on contact changed to a new location, randomly chosen from nine positions arranged on a regular grid (Fig. 1C), with a minimal distance of 7.6 cm between two target positions. For experiments with subject S6, the target position was chosen freely within the workspace, with the only restriction of a minimal distance of 7.5 cm to the previous target. The radius of the circular target was 1.85 cm and that of the cursor 1.23 cm. The resulting workspace was about 20 cm × 20 cm wide (for both, hand and cursor). Target positions, times of target appearance and continuous cursor positions were recorded synchronized to the neuronal signals. During one session, between 80 and 226 (average: 181) target reaches were carried out by the subjects. A session lasted between 80 and 300 s (average: 167). Each subject performed between four and five sessions in total. Subject S3 took part in an additional set of experiments (four sessions) after implantation of additional electrodes.
Display Full Size version of this image (98K) Fig. 1. (A) MRT reconstruction of electrode locations in subject 6. Electrodes are marked in color according to responses upon electrical stimulation through the electrodes (orange: arm, red: hand, blue: leg, green: eye, yellow: oro-facial). Circles depict sensory responses and filled markers motor responses. The central sulcus (CS) is shown by the dotted white line. (B) Photograph of an ECoG electrode grid placed directly on the cortex, taken during surgery for implantation. (C) Illustration of the experimental task: The green curve represents the cursor trajectory within 4 s of movement, following a sequence of six target positions, indicated by the yellow numbers. Possible positions, arranged on a regular grid, are indicated by the dotted white circles. To the subjects, however, only the green cursor and the current yellow target were visible, not the cursor trace and the potential target positions. (D) Examples of recorded data from two ECoG channels (gray), their low pass filtered versions (red), their γ-band (40–80 Hz) amplitudes (orange) and synchronously recorded x- and y-positions of the cursor (green and blue). Thin dotted lines depict target positions. Data are from the same 4 s as the cursor trace in C.
For decoding we assumed that the four-dimensional hand state xt, consisting of hand x-/y-position and velocity, evolved according to the following linear stochastic difference equation:
State model:
Measurement model:
yt=H xt+n+vt xt+n+vt | (2) |
To predict movement trajectories from measured neuronal activity, we need to estimate the probability density of the hand state xt at time t, given the history of observed ECoG signal vectors p(xt|{y1, …, yt}). The mean of this density is considered as the predicted hand state ![]() . Since the time-invariant state space model defined by Eqs. (1) and (2) is linear and Gaussian, this probability density is also Gaussian ([Anderson and Moore, 1979] and [Harvey, 1989]) and is therefore completely defined by its mean xt and covariance Pt at time t. Using this fact, it is possible to derive (see e.g. [Anderson and Moore, 1979] and [Harvey, 1989])
an efficient recursion for the estimation of the probability density,
the so-called Kalman filter. The Kalman filter proceeds in two steps.
The first step is the “prediction step” – this yields a first estimate
of the mean and covariance matrix of the hand state at time t according to the linear transition Eq. (1) of the hand:
. Since the time-invariant state space model defined by Eqs. (1) and (2) is linear and Gaussian, this probability density is also Gaussian ([Anderson and Moore, 1979] and [Harvey, 1989]) and is therefore completely defined by its mean xt and covariance Pt at time t. Using this fact, it is possible to derive (see e.g. [Anderson and Moore, 1979] and [Harvey, 1989])
an efficient recursion for the estimation of the probability density,
the so-called Kalman filter. The Kalman filter proceeds in two steps.
The first step is the “prediction step” – this yields a first estimate
of the mean and covariance matrix of the hand state at time t according to the linear transition Eq. (1) of the hand:
Prediction step:
In
the second step, the “update step”, the mean and covariance matrix of
the one-step predictor are corrected, taking the measured neuronal
activity into account, to obtain the final mean ![]() and covariance
and covariance ![]() :
:
Update step:
As neuronal activity yt we used the low-pass filtered ECoG signals: Signals were smoothed with a Savitzky-Golay filter (3rd order, 0.75 s width). The neuronal signal vector yt at time t contained the smoothed signals of all decoded electrodes at time t–τ. Thus, a positive value of τ reflects neuronal activity preceding movement. We tested different values for τ, ranging from 0 ms to 625 ms, in steps of 1/16 s (62.5 ms).
We used a four-dimensional state space xt, consisting of horizontal and vertical position (Cartesian coordinates) and horizontal and vertical velocity. The ECoG-signals were correlated to all these movement parameters. By use of the Kalman filter, also the correlation to velocity can contribute to the prediction of hand position, since the linear relationship between different state variables is given through F in the state model (Eq. (1)) and is exploited in the prediction step (Eq. (3)). In that way, including velocity in the filter process can improve the performance of position decoding.
We predicted movement trajectories, i.e. the x-/y-positions of the cursor in time steps of 62.5 ms (i.e. 16 Hz sampling), from the ECoG signals recorded during arm movements. Predictions were made using mutually exclusive test and training data sets: While one-fourth of an experimental session was used as a test set for decoding, all remaining recordings from the same subject and recording day were used as training set to determine the model parameters. For the computation of averages and standard deviations, the measures from each part were weighted by the amount of decoded data in that part.
For the evaluation of prediction performance, we calculated the Pearson correlation coefficients between predicted and measured (x- and y-) positions individually for each coordinate and each test set. In the following all presented correlation coefficients are averages across all test sets, in Fig. 4and Fig. 5 we also averaged the coefficients of both coordinates (x and y).
In
each prediction period, we assumed the starting position (but not the
velocity) to be known, meaning that it was preset in the x- and y- position entries of the vector ![]() .
Further on, position was decoded continuously until the end of the
prediction period. Evaluation of decoding performance was restricted to
the time period where the Kalman filter remained in a stable state,
i.e. when the Kalman gain Kt had approached a constant level. The temporal evolution of Kt as well as Pt is illustrated in Fig. 2.
Observe that at about 1–2 s after the beginning of a test session,
the Kalman gain and the error covariance reached a stable state and
were no longer subject to significant changes. This represents an
optimal balance between the state and the observation model for the
given amount of observational (i.e. neuronal) and state noise.
.
Further on, position was decoded continuously until the end of the
prediction period. Evaluation of decoding performance was restricted to
the time period where the Kalman filter remained in a stable state,
i.e. when the Kalman gain Kt had approached a constant level. The temporal evolution of Kt as well as Pt is illustrated in Fig. 2.
Observe that at about 1–2 s after the beginning of a test session,
the Kalman gain and the error covariance reached a stable state and
were no longer subject to significant changes. This represents an
optimal balance between the state and the observation model for the
given amount of observational (i.e. neuronal) and state noise.
Display Full Size version of this image (17K) Fig. 2. Temporal evolution of the Kalman filter during prediction. Left panel: Development of the coefficients in the Kalman gain Kt over the first 3 s of a session. Different shades represent coefficients associated with position (black) and velocity (gray). All coefficients reach a stable state after about 1–2 s. Right panel: development of the Eigen-values of the error covariance matrix of the prediction Pt over the same time. Again after about 1–2 s a stable state is reached. All traces (Kalman gain coefficients and Eigen-values of the error covariance) are aligned to their values after reaching a stable state (marked as ‘s’) in which both, Kt and Pt, change no more than marginally.
In one analysis we used the low-pass filtered ECoG signals as neuronal features in yt. To extract this feature, which we termed the low-frequency component (LFC), the raw ECoG signals were smoothed with a Savitzky-Golay filter (2nd order, 0.5 s width). The Savitzky-Golay filter was applied such that only signals before the current movement time were used, in order to avoid contributions from signals following that instant of movement and thus to minimize possible influences by proprioception in the decoding. The neuronal signal vector yt at time t contained the smoothed signals of all decoded electrodes at time t–τ. Thus, a positive value of τ reflects neuronal activity preceding movement. Lacking prior knowledge we tested different values for τ, ranging from 0 ms to 750 ms. The use the LFC was motivated by successful use for the decoding of movement trajectories and directions from LFP signals ([Mehring et al., 2003] and [Rickert et al., 2005]) and decoding of movement direction from ECoG ([Mehring et al., 2004] and [Ball et al., under revision]). In these studies, the directional information of the LFC of ECoG/LFP was higher than the directional information of features based on higher frequency signal components. It was also found to be the most informative signal part of ECoG in the study of Schalk et al. (2007), where it was called the local motor potential (LMP).
In another analysis we used amplitude modulations of different frequency bands as neuronal feature for decoding. Amplitudes were extracted by using the Hilbert transform (e.g. Bruns, 2004): First, the raw ECoG signals were band pass filtered (5th order Butterworth filter), then the resulting signals were Hilbert transformed to obtain the so-called analytic signal. To extract the amplitude one has to take the magnitude of the complex valued analytic signal. Finally, the resulting amplitude modulations were smoothed by a Savitzky-Golay filter (2nd order, 0.5 s width). By choosing different frequency ranges in the band pass filter the amplitude modulations of different frequency bands can be extracted. It should be noted that the band pass filter was such that only signals before the current movement time were used, in order to avoid contributions from signals following that instant of movement and thus to minimize possible influences by proprioception in the decoding. For decoding we used amplitude modulations exclusively as also in conjunction with the LFC.
First, we predicted movement trajectories from the low pass filtered ECoG signals. Examples of real and predicted movements over a time of 15 s are shown in Fig. 3. Predicted and actual movement trajectories did not match perfectly but the predicted movement trajectories were an approximate reconstruction of the actually performed movements. To get a better impression of the quality of the movement prediction an animated reconstruction of the actual and the predicted cursor movement is presented in the supplementary material.
Display Full Size version of this image (114K) Fig. 3. Examples of predicted movement trajectories. Real trajectories of 15 s length are given by black traces and predicted trajectories overlaid in gray. Left two columns: x- and y-positions; right two columns: x- and y-velocity in the same time period as for positions. For each subject (rows), one example is given. Correlation coefficients (CC) for the plotted time period are shown in the upper left corner of each plot.
Decoding was tested for a set of different temporal delays τ between neuronal activity and movement, ranging from 0 ms to 750 ms (see Section 2). A positive delay τ indicates the time by which neuronal activity used for decoding, preceded the movement. In Fig. 4A, we show the average correlation coefficients between real and predicted hand position in dependence of τ. The optimal delay was slightly different for each subject, but generally the optimal prediction performance was found at short delays. On average across all subjects, a delay of 93.75 ms (=3/32 s) was found best when movement prediction used the LFC. Thus, further results presented here were computed using a fixed τ = 93.75 ms without any further optimization.
Display Full Size version of this image (29K) Fig. 4. Prediction accuracy of position for different temporal delays τ between movement and neuronal activity. Positive values indicate that neuronal data preceded movement. Prediction performance is given by the average (over sessions and both coordinate axes) correlation coefficient between measured and predicted x- and y-positions of the cursor. Each colored line depicts the results from one subject (S1–S6). The black line shows the average across subjects. (A) Prediction from the low frequency component (LFC). The light gray bar indicates the value of τ that produced the best prediction in the average over all subjects at 93.75 ms (3/32 s). This was then used as a common value for all subjects in further analysis. (B) Prediction from a feature space comprising both, LFC and γ-amplitudes from a 40–80 Hz band.
We studied the use of amplitude modulation in higher frequencies by first evaluating a sequence of bands of 10 Hz width, centered around 5 to 95 Hz, in steps of 10 Hz. We excluded frequencies higher than 100 Hz from the analysis because from two of our subjects, data was recorded with a sampling rate of only 256 Hz, preventing analysis of very high frequencies. Fig. 5A presents the accuracy of position prediction from those bands for all subjects. Results vary considerably across subjects, yet a broad band in the γ-range showed the highest decoding accuracy among all frequencies higher than those, corresponding to the LFC. Decoding from amplitudes extracted from a band of 40–80 Hz yielded a similar dependence on the temporal delay τ as the decoding from LFC (see Fig. 5B). However, in combination with the LFC features, γ-activity 40–80 Hz did not significantly improve the prediction of hand positions, as shown in Fig. 4B. In the following, we therefore report results based on decoding the LFC alone.
Display Full Size version of this image (29K) Fig. 5. Prediction accuracy of position for amplitudes of different frequency bands. Results are averaged over all sessions. Each colored line depicts the results from one subject (S1–S6). The black line shows the average across subjects. (A) Scan over different frequency bands of 10 Hz width, up to 100 Hz. Results differ largely for different subjects (colors as in Fig. 3), but on the average low frequencies and frequencies in the γ-range yield the highest accuracy. (B) Prediction accuracy for decoding from amplitudes of the 40–80 Hz band for different delays τ.
In our recordings, the ECoG signals were correlated to several movement parameters, including position, velocity and acceleration. As these parameters bear a relation to each other, combining them within the state model of a Kalman filter may improve the decoding accuracy of each individual movement parameter. Thus, the prediction accuracy for position might be increased by also using velocity and/or acceleration in the state space. On the other hand, a higher-dimensional state space implies more parameters in the model relating neuronal activity to movement (Eq. (2)) and thereby, the estimation of these parameters becomes less reliable. This might decrease the decoding accuracy. In order to investigate this tradeoff, we calculated the prediction accuracy for different state spaces (see Table 2): position only; position and velocity; position and acceleration; position, velocity and acceleration. As neuronal feature, the LFC of the ECoG at a delay of 93.75 ms before the movement was used. A state space comprising position and velocity yielded the best predictions with a slightly higher performance than a state space additionally including acceleration, and a much higher performance than state spaces consisting of only position or position and acceleration. We therefore decided to use a four-dimensional state space model, comprised of x-/y-position and velocity.
Prediction accuracies for different state space compositions
State space composition Position Position, velocity Position, acceleration Position, velocity, acceleration S1 0.11 0.23 0.11 0.19 S2 0.05 0.29 0.05 0.24 S3 0.05 0.16 0.04 0.12 S4 0.29 0.42 0.27 0.42 S5 0.22 0.42 0.21 0.39 S6 0.26 0.45 0.25 0.44 0.16 0.33 0.16 0.30 Values given for each state space composition and subject reflect correlation coefficients between real and predicted positions, averaged over all test sets and averaged over correlation coefficients for x- and y-position. The last row depicts the average across subjects.
Fig. 6 shows an overview over the prediction accuracy for x-/y-position and velocity for all subjects. Four subjects (S3–S6) had electrodes implanted above parts of the primary motor area, including regions related to arm and hand movement, as was confirmed by electrical stimulation. Three of them (S4, S5 and S6) yielded notably better decoding results than the other subjects (S1, S2) who had no electrodes implanted over parts of primary motor cortex related to arm or hand movement. For S3 however, decoding performance was relatively weak, in spite of having electrodes placed favorably over hand/arm motor cortex. A likely reason is the abundance of interictal epileptic activity on most of the channels of S3.
Display Full Size version of this image (28K) Fig. 6. Overview of decoding performance for LFC signals, using a fixed temporal delay of 93.75 ms. Performance is measured by the (weighted) average correlation coefficient between the real and predicted hand position (dark grey bars) and velocity (light gray bars). Weighting was done to take the different length of the sessions into account. Left and right bars of one shade represent measures for position and velocity in the horizontal (x-) and vertical (y-) direction, respectively. White bars show a control measure, where x- and y-position were predicted from a random signal (noise) with the same auto-correlation as the LFC data for each subject. Error bars denote the (weighted) standard deviation. (A) Subjects S4–S6 had electrodes placed over hand/arm motor cortex, which represents the optimal recording site for arm movement decoding (see Fig. 7). Furthermore no strong epileptic activity contaminated the signal, allowing for a decent decoding accuracy. (B) For subjects S1–S3 only suboptimal recordings were available for analysis. (*) S1 and S2 had no electrodes implanted over hand/arm motor cortex. (**) Recordings of S3 were compromised by strong interictal epileptic activity on almost all recording sites, which probably accounts for the low prediction performance.
As a control we computed the prediction performance that can be obtained by chance. To this end, random signals with the same auto-correlation as the ECoG signals were generated and then filtered and decoded in the same way as the ECoG. To ensure a realistic auto-correlation of the random signals, the raw ECoG signals were Fourier transformed, the phases were set to a uniform random variable, and the result was transformed back to the time domain by an inverse Fourier transformation. The prediction performance for the random signals (white bars in Fig. 6), indicate that the correlation coefficient for a random signal with the same auto-correlation as the ECoG signals was close to zero and thus, correlations between real and predicted hand trajectories obtained from the ECoG really stem from informational content in the ECoG rather than from general signal properties.
In a separate analysis, we investigated the origin of the decoded signals. For this purpose, we calculated the decoding performance, measured by the average correlation coefficient of all test sets (as described in Methods), but using only signals from small subregions of the cortex. Results from those subregions were mapped on the area that was covered by the electrode grid, yielding a spatial map of the prediction performance (see Fig. 7). Since the decoding performance, obtained from the measurement of a single ECoG-electrode, was very weak, we evaluated the performances obtained by using the signals from all possible square quartets of adjacent electrodes. To assign significance values to the average correlation coefficients, we calculated the probability for the null hypothesis of no positive average correlation for each quartet on the basis of the standard-error of the mean (assuming a normal distribution of prediction values across test sets). The grey contours in Fig. 7 indicate the areas of significant positive correlations.
Display Full Size version of this image (97K) Fig. 7. Topographies of prediction performance, measured by the correlation coefficient. Prediction performance is plotted in color code over the area of the electrode grids. Decoding was based on the signals from quartets of neighboring electrodes; the correlation coefficient was then interpolated over the whole grid area. Functional anatomical areas are given by the results of electric stimulation through the implanted electrodes: motor responses (pink letters) and sensory responses (white letters) at the hand (H), arm (A), shoulder (S), leg (L), oro-facial (O) or eyes (E). The approximate location of the central sulcus, determined from the individual anatomical MRI scans, is indicated by the white dashed lines. Gray arrows beneath each graph point rostrally. Gray contours on the maps outline regions where the average correlation coefficients was significantly (p < 0.01, determined through the standard error of the mean) above zero. Top row: topographies for decoding from the low frequency component (LFC). Bottom row: topographies for decoding from γ-activity (40–80 Hz).
For decoding from the LFC (upper row of images in Fig. 7), sites with high correlations were found in arm and parts of hand motor areas, where available, but also in other motor areas, where no hand/arm responses to electrical stimulation were found. Also, some non-primary motor areas allowed for movement prediction, in particular pre-motor areas, but also parietal and somatosensory cortex. For a prediction from activity in the γ-band sites of good decoding were more focal, but also with highest correlations in hand and arm motor cortex if available. Note that for interpreting the decoding topographies, the variability over sessions should be taken into account. Overall, the distribution of correlation coefficients over cortical areas should be considered qualitatively rather than quantitatively, and positions of high correlations only as approximate regions with high informational content.
Control over continuous states is an important modality for brain-machine interfacing, as it is more flexible and generalized than a control based on the classification of discrete states. In other ECoG- or EEG-based BMI applications, continuous control was either achieved by willingly modulating the amplitude of naturally occurring rhythms of the brain (e.g. Leuthardt et al., 2006), or by creating a continuous control variable from a discrimination of originally discrete states (e.g. Blankertz et al., 2006). With single-unit activity ([Taylor et al., 2002] and [Wu et al., 2006]) or local field potentials (Mehring et al., 2003) recorded from monkeys, however, continuous decoding has been achieved directly by using the activity related to hand/arm movement trajectories. Here, we show that the ECoG in humans also contains information on continuous two-dimensional hand movement trajectories and might therefore be used for BMI control in a similar manner as multiple single-unit or LFP activity.
The task we chose allowed for a large variety of different movement trajectories. In total, the paradigm allowed for 72 different combinations of start- and end-targets. Yet, there was no clear separation into distinct trials. Movements were continuous over a whole recording session in the sense that no conceivable hold periods of hand position occurred. This allows for better generalization over the entire workspace than a task with only a small number of stereotyped movements (e.g. [Taylor et al., 2002], [Mehring et al., 2003] and [Schalk et al., 2007]). The predicted movement trajectories approximately reproduced the actually performed trajectories (cf. Fig. 5). Prediction accuracy was best in those cases were recordings were available from the electrically excitable part of the hand/arm motor cortex without being heavily contaminated by frequent epileptic potentials. Therefore, our results clearly demonstrate that ECoG signals provide useful information regarding the entire two dimensional movement trajectories.
As neuronal feature for decoding, we
primarily used the low frequency component (LFC) of the ECoG. This
signal component is already well established as providing information
about movements in previous studies, as was shown for directional
classification from ECoG ([Mehring et al., 2004] and [Ball et al., under revision]) and for the prediction of entire trajectories from LFP (Mehring et al., 2003), and very recently from ECoG (Schalk et al., 2007). Nevertheless, other signal components, e.g. amplitudes of higher frequency bands ([Leuthardt et al., 2004], [Rickert et al., 2005], [Schalk et al., 2007] and [Ball et al., under revision]),
can provide additional information about movements. In fact, we also
used amplitude modulations of different frequency bands for decoding
and our results show that the γ-band yields the highest decoding
accuracy among frequency bands above the low-frequency component (i.e.
> 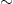 10 Hz).
Using the γ-band in conjunction with the LFC, however, did not
significantly increase the prediction accuracy. Our study was
restricted to frequency bands below 100 Hz, since for two of our
subjects recordings were only available at a sampling rate of
256 Hz, and it might be that frequency bands above 100 Hz
carry additional information about movement (cf. Schalk et al., 2007). Therefore, the optimal choice of frequency bands for the decoding of trajectories still deserves further investigation.
10 Hz).
Using the γ-band in conjunction with the LFC, however, did not
significantly increase the prediction accuracy. Our study was
restricted to frequency bands below 100 Hz, since for two of our
subjects recordings were only available at a sampling rate of
256 Hz, and it might be that frequency bands above 100 Hz
carry additional information about movement (cf. Schalk et al., 2007). Therefore, the optimal choice of frequency bands for the decoding of trajectories still deserves further investigation.
How
does our prediction performance, based on recordings with relatively
large and widely spaced epicortical electrodes (4 mm diameter with
10 mm center-to-center inter-electrode distance; cf. Methods) in
humans, compare to the performance obtained from intra-cortical
microelectrode recordings in monkeys� Wu et al. (2006)
used a Kalman filter approach in a similar task to decode
two-dimensional trajectories from firing rates of 42 single units
(single unit activity, SUA). In continuous trials of 1 min length
they obtained average correlation coefficients of 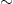 0.88
for hand position, which is substantially higher than in our study
where the average correlation coefficient was 0.43 for subjects with
coverage of hand/arm motor cortex and without strong interictal
epileptic activity. However, spiking activity is not easily recorded in
a stable manner for long time periods, requires appropriate algorithms
for spike sorting, and many electrodes are needed to record the spiking
activity of such a large number of units simultaneously. For field
potentials, the difference between our results using epicortical
recordings and previous results using intracortical recordings seems to
be smaller: Mehring et al. (2003)
used a support-vector regression on intracortical local field
potentials (LFP) from eight electrodes in both hemispheres and obtained
average correlation coefficients of
0.88
for hand position, which is substantially higher than in our study
where the average correlation coefficient was 0.43 for subjects with
coverage of hand/arm motor cortex and without strong interictal
epileptic activity. However, spiking activity is not easily recorded in
a stable manner for long time periods, requires appropriate algorithms
for spike sorting, and many electrodes are needed to record the spiking
activity of such a large number of units simultaneously. For field
potentials, the difference between our results using epicortical
recordings and previous results using intracortical recordings seems to
be smaller: Mehring et al. (2003)
used a support-vector regression on intracortical local field
potentials (LFP) from eight electrodes in both hemispheres and obtained
average correlation coefficients of 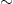 0.7
for short trajectories (about 1 s) of restricted and stereotyped
movements (center-out movements). In both of the above studies ([Mehring et al., 2003] and [Wu et al., 2006]),
electrodes were specifically placed in the arm area of the monkey motor
cortex, whereas in our case, electrodes were placed according to the
requirements of the clinical epilepsy evaluation. Moreover, recordings
from smaller epicortical electrodes arranged in denser grids could
possibly further improve the ECoG prediction performance.
0.7
for short trajectories (about 1 s) of restricted and stereotyped
movements (center-out movements). In both of the above studies ([Mehring et al., 2003] and [Wu et al., 2006]),
electrodes were specifically placed in the arm area of the monkey motor
cortex, whereas in our case, electrodes were placed according to the
requirements of the clinical epilepsy evaluation. Moreover, recordings
from smaller epicortical electrodes arranged in denser grids could
possibly further improve the ECoG prediction performance.
The only other study to date investigating the prediction of movement trajectories from ECoG in humans (Schalk et al., 2007) yielded an average correlation for position of 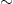 0.5
in five subjects that all had good electrode coverage of the motor
cortex. This is similar to the prediction accuracy we obtained (average
correlation coefficient of 0.43) for comparable subjects. However, Schalk et al. (2007)
used relatively restricted circular tracking movements. In our study,
less restricted, target-directed, full two-dimensional movements at
varying speeds were performed and therefore, we extend the
investigation of Schalk et al. (2007) to more complex movements.
0.5
in five subjects that all had good electrode coverage of the motor
cortex. This is similar to the prediction accuracy we obtained (average
correlation coefficient of 0.43) for comparable subjects. However, Schalk et al. (2007)
used relatively restricted circular tracking movements. In our study,
less restricted, target-directed, full two-dimensional movements at
varying speeds were performed and therefore, we extend the
investigation of Schalk et al. (2007) to more complex movements.
How much do our predictions depend on eye movements (e.g. caused by target appearance or cursor movement) or on sensory input (e.g. somatosensory or proprioceptive), rather than intended motor output� Decoding topographies (Fig. 7) suggest that predictions in S3–S6 were primarily achieved by signals from arm or hand motor areas, less by somatosensroy areas and only very little by areas related to eye movement. While sensory influence cannot be completely ruled out, it should be noted that neuronal activity before the actual movement was used for decoding, i.e. before the proprioceptive feedback of the predicted movement, disqualifying it as the primary source of the decoded signals. This important issue may, however, be more thoroughly addressed in experiments with direct visual feedback of the prediction itself, without real hand movement of the subject: If in that case control was successfully achieved via brain signals alone, a role of somatosensory input or proprioception would be highly unlikely ([Levine et al., 2000], [Leuthardt et al., 2004], [Leuthardt et al., 2006] and [Blankertz et al., 2006]).
Based on other experiments with online feedback, we also expect further amplification of predictive signal components when subjects learn to control a cursor by means of their brain signals (e.g. [Taylor et al., 2002] and [Carmena et al., 2003]). Therefore, the two-dimensional cursor control based on the signals investigated in this study might, in fact, yield a precise and continuous BMI control modality. The present study serves as a first step towards this goal by showing the principal usefulness of arm movement related ECoG signals for such a control paradigm. A final decision concerning the usefulness of our approach for BMI application can only be made after experiments with online feedback of predictions.
This work was supported by the German Federal Ministry of Education and Research (BMBF grant 01GQ0420 to BCCN Freiburg) and by the WIN-Kolleg of the Heidelberg Academy of Sciences and Humanities.
Anderson and Moore, 1979 B.D.O. Anderson and J.B. Moore, Optimal filtering, Prentice-Hall, Englewood Cliffs, NJ (1979).
Ball et al., 2004 Ball T, Nawrot MP, Pistohl T, Aertsen A, Schulze-Bonhage A, Mehring C Towards an implantable brain-machine interface based on epicortical field potentials. Biomedizinische Technik, Biomedical Engineering, 38. Jahrestagung der Deutschen Gesellschaft für Biomedizinische Technik im VDE - BMT 2004; 49: 756-9.
Ball et al., under revision Ball T, Schulze-Bonhage A, Aertsen A, Mehring C. Differential Representation of Arm Movement Direction in the Electrocorticogram of the Human Frontal Lobe, under revision.
Birbaumer et al., 1999 N. Birbaumer, N. Ghanayim, T. Hinterberger, I. Iversen, B. Kotchoubey, A. Kubler, J. Perelmouter, E. Taub and H. Flor, A spelling device for the paralysed, Nature 398 (1999), pp. 297–298. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (195)
Blankertz et al., 2006 B. Blankertz, G. Dornhege, M. Krauledat, K.R. Muller, V. Kunzmann, F. Losch and G. Curio, The Berlin Brain-Computer Interface: EEG-based communication without subject training, IEEE Trans Neural Syst Rehabil Eng 14 (2006), pp. 147–152. Full Text via CrossRef
Blankertz et al., 2003 B. Blankertz, G. Dornhege, C. Schafer, R. Krepki, J. Kohlmorgen, K.R. Muller, V. Kunzmann, F. Losch and G. Curio, Boosting bit rates and error detection for the classification of fast-paced motor commands based on single-trial EEG analysis, IEEE Trans. Neural Syst. Rehabil Eng 11 (2003), pp. 127–131. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (40)
Bruns, 2004 A. Bruns, Fourier-, Hilbert- and wavelet-based signal analysis: are they really different approaches�, J Neurosci Methods 137 (2) (2004), pp. 321–332. SummaryPlus | Full Text + Links | PDF (280 K) | View Record in Scopus | Cited By in Scopus (35)
Carmena et al., 2003 J.M. Carmena, M.A. Lebedev, R.E. Crist, J.E. O’Doherty, D.M. Santucci, D.F. Dimitrov, P.G. Patil, C.S. Henriquez and M.A. Nicolelis, Learning to control a brain-machine interface for reaching and grasping by primates, PLoS Biol 1 (2003), p. E42.
Georgopoulos et al., 1982 A.P. Georgopoulos, J.F. Kalaska, R. Caminiti and J.T. Massey, On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex, J Neurosci 2 (1982), pp. 1527–1537. View Record in Scopus | Cited By in Scopus (405)
Guger et al., 2000 C. Guger, H. Ramoser and G. Pfurtscheller, Real-time EEG analysis with subject-specific spatial patterns for a brain-computer interface (BCI), IEEE Trans Rehabil Eng 8 (2000), pp. 447–456. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (41)
Harvey, 1989 A. Harvey, Forecasting, structural time series models and the Kalman filter, Cambridge University Press, Cambridge (1989).
Hochberg et al., 2006 L.R. Hochberg, M.D. Serruya, G.M. Friehs, J.A. Mukand, M. Saleh and A.H. Caplan et al., Neuronal ensemble control of prosthetic devices by a human with tetraplegia, Nature 442 (2006), pp. 164–171. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (94)
Kennedy et al., 2004 P.R. Kennedy, M.T. Kirby, M.M. Moore, B. King and A. Mallory, Computer control using human intracortical local field potentials, IEEE Trans Neural Syst Rehabil Eng 12 (2004), pp. 339–344. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (20)
Leuthardt et al., 2006 E.C. Leuthardt, K.J. Miller, G. Schalk, R.P. Rao and J.G. Ojemann, Electrocorticography-based brain computer interface—the Seattle experience, IEEE Trans Neural Syst Rehabil Eng 14 (2006), pp. 194–198. Full Text via CrossRef
Leuthardt et al., 2004 E.C. Leuthardt, G. Schalk, J.R. Wolpaw, J.G. Ojemann and D.W. Moran, A brain-computer interface using electrocorticographic signals in humans, J. Neural Eng 1 (2004), pp. 63–71. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (69)
Levine et al., 2000 S.P. Levine, J.E. Huggins, S.L. BeMent, R.K. Kushwaha, L.A. Schuh, M.M. Rohde, E.A. Passaro, D.A. Ross, K.V. Elisevich and B.J. Smith, A direct brain interface based on event-related potentials, IEEE Trans Rehabil Eng 8 (2000), pp. 180–185. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (61)
Mehring et al., 2004 C. Mehring, M.P. Nawrot, S.C. de Oliveira, E. Vaadia, A. Schulze-Bonhage and A. Aertsen et al., Comparing information about arm movement direction in single channels of local and epicortical field potentials from monkey and human motor cortex, J Physiol Paris 98 (2004), pp. 498–506. Abstract | Full Text + Links | PDF (454 K) | View Record in Scopus | Cited By in Scopus (6)
Mehring et al., 2003 C. Mehring, J. Rickert, E. Vaadia, O.S. Cardosa de, A. Aertsen and S. Rotter, Inference of hand movements from local field potentials in monkey motor cortex, Nat Neurosci 6 (2003), pp. 1253–1254. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (48)
Moran and Schwartz, 1999 D.W. Moran and A.B. Schwartz, Motor cortical representation of speed and direction during reaching, J Neurophysiol 82 (1999), pp. 2676–2692. View Record in Scopus | Cited By in Scopus (150)
Pesaran et al., 2002 B. Pesaran, J.S. Pezaris, M. Sahani, P.P. Mitra and R.A. Andersen, Temporal structure in neuronal activity during working memory in macaque parietal cortex, Nat Neurosci 5 (2002), pp. 805–811. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (132)
Rickert et al., 2005 J. Rickert, S.C. Oliveira, E. Vaadia, A. Aertsen, S. Rotter and C. Mehring, Encoding of movement direction in different frequency ranges of motor cortical local field potentials, J Neurosci 25 (2005), pp. 8815–8824. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (26)
Schalk et al., 2007 G. Schalk, J. Kubánek, K.J. Miller, N.R. Anderson, E.C. Leuthardt and J.G. Ojemann et al., Decoding two-dimensional movement trajectories using electrocorticographic signals in humans, J Neural Eng 4 (2007), pp. 264–274.
Scherberger et al., 2005 H. Scherberger, M.R. Jarvis and R.A. Andersen, Cortical local field potential encodes movement intentions in the posterior parietal cortex, Neuron 46 (2005), pp. 347–354. SummaryPlus | Full Text + Links | PDF (388 K) | View Record in Scopus | Cited By in Scopus (38)
Serruya et al., 2002 M.D. Serruya, N.G. Hatsopoulos, L. Paninski, M.R. Fellows and J.P. Donoghue, Instant neural control of a movement signal, Nature 416 (2002), pp. 141–142. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (252)
Taylor et al., 2002 D.M. Taylor, S.I. Tillery and A.B. Schwartz, Direct cortical control of 3D neuroprosthetic devices, Science 296 (2002), pp. 1829–1832. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (300)
Thach, 1978 W.T. Thach, Correlation of neural discharge with pattern and force of muscular activity, joint position, and direction of intended next movement in motor cortex and cerebellum, J Neurophysiol 41 (1978), pp. 654–676. View Record in Scopus | Cited By in Scopus (114)
Wolpaw and McFarland, 2004 J.R. Wolpaw and D.J. McFarland, Control of a two-dimensional movement signal by a noninvasive brain-computer interface in humans, Proc Natl Acad Sci USA 101 (2004), pp. 17849–17854. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (103)
Wolpaw et al., 2000 J.R. Wolpaw, D.J. McFarland and T.M. Vaughan, Brain-computer interface research at the Wadsworth Center, IEEE Trans Rehabil Eng 8 (2000), pp. 222–226. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (86)
Wu et al., 2006 W. Wu, Y. Gao, E. Bienenstock, J.P. Donoghue and M.J. Black, Bayesian population decoding of motor cortical activity using a Kalman filter, Neural Comput 18 (2006), pp. 80–118. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (21)
 (6313 K)
(6313 K)
mmc1.avi 
AVI movie 1.
Movie
1. Animated 2D prediction example from subject 4. Left: The green
dot and trace describe the real hand position, red the prediction based
on low-pass filtered ECoG signals. Right: Low-pass filtered ECoG
signals, color-coded interpolation over the area of the epi-cortical
electrode grid. Magenta and white letters denote motor and
somatosensory contacts, respectively (as confirmed by electrical
stimulation). The animation reflects the actual speed of the movements.
 (6431 K)
(6431 K)
mmc2.avi 
AVI movie 2.
Movie 2. Animated 2D prediction example from subject 5. (also see description for subject 4)  (10275 K)
(10275 K)
mmc3.avi 
AVI movie 3.
Movie 3. Animated 2D prediction example from subject 6. (also see description for subject 4)
 Corresponding author at: Bernstein Center for Computational Neuroscience, Albert-Ludwigs-University, Freiburg, Germany. Tel.:
Corresponding author at: Bernstein Center for Computational Neuroscience, Albert-Ludwigs-University, Freiburg, Germany. Tel.: 
|
Journal of Neuroscience Methods
Volume 167, Issue 1, 15 January 2008, Pages 105-114 Brain-Computer Interfaces (BCIs) |
|
|