Keywords: Coefficient of variation; Cortical variability; Gamma process; Fano factor; Monkey motor cortex; Noise current injection; Renewal process, Spiking irregularity

Article Outline

1. Introduction

2. Methods

2.1. Point process theory

2.1.1. Renewal point processes

2.1.2. Gamma processes

2.1.3. Operational time and rate modulation

2.1.4. Empirical measures of irregularity and variability

2.2. In vitro current injection experiments

2.3. Monkey experiment

3. Results

3.1. Bias and variance of estimation

3.1.1. Spike train irregularity

3.1.2. Spike count variability

3.1.3. Variance of the estimator

3.2. Measuring irregularity in presence of rate modulation

3.3. Irregularity vs. count variability

3.4. Time resolved joint analysis of irregularity and count variability

3.4.1. Rate modulated gamma simulation

3.4.2. Modulated synaptic input currents in vitro

3.4.3. Single unit recording in monkey motor cortex

4. Discussion

4.1. Operational time vs. real time

4.2. Renewal assumption

4.3. Equilibrium condition

4.4. Refractory period

4.5. Non-stationarity across trials

4.6. Variability in cortical neurons

Acknowledgements

References

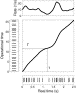Display Full Size version of this image (28K)

Fig. 1. Transformation of time. A renewal process of unit rate is simulated in operational time (vertical panel). A spike event at time t^′ is translated into a spike event in real time t by the time transformation (center panel, Eq. (2)) given by the integral of the rate function (top panel). Conversely, a rate modulated realization of a point process may be demodulated by mapping an event in real time t onto the corresponding event in operational time t^′.

Display Full Size version of this image (39K)

Fig. 2. Noise current injection. (a) Excitatory (top) and inhibitory (bottom) presynaptic events were generated as independent Poisson processes. Each event contributed a single EPSC or IPSC to the total current (black curve), carrying a net charge of 0.09 and −0.18 pQ, respectively. (b) Membrane potential of a layer 5 pyramidal cell (top) measured during the injection of a fluctuating current (bottom) that replaced excitatory and inhibitory synaptic input.

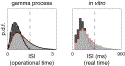Display Full Size version of this image (13K)

Fig. 3. Inter-spike interval distribution for finite observation time. Analytical and simulated distributions for a gamma-process (left) and empirical distributions from a layer 5 pyramidal neuron recorded in vitro (right). The light gray histogram in the left panel displays the probability density f(x) constructed from 10⁵ intervals randomly drawn from a gamma distribution (α=2.8). The dark gray histogram shows the modified distribution for a finite observation interval of length 1.5 in operational time. Solid lines show the corresponding analytical results (Eqs. (3) and (6)). The gamma order of 2.8 was estimated as α=1/CV² from the full distribution in vitro (light gray histogram, right), constructed from 4181 intervals recorded during 1150 s. Short observations of length 415 ms (1.5 times the mean interval length) yielded the dark gray in vitro histogram.

Display Full Size version of this image (46K)

Fig. 4. Dependence of interval statistics on observation length. All times are specified in operational time. For gamma processes (left), all three statistical measures of mean interval μ (top), variance of intervals σ² (middle), and squared coefficient of variation CV² (bottom) show a monotonic dependence on the width T^′ of the analysis window. Shown are the analytic (gray lines) and simulation (thin black lines) results for gamma processes of order α=0.25, 0.5, 1, 2, 4. In the right panels we show the empiric results from five pyramidal neurons that were stimulated with mixed excitatory/inhibitory shotnoise currents. The more irregular the process is, the more slowly the CV² approaches the asymptotic limit of 1/α for T^′→∞. The Poisson process (dashed gray line) saturates at about T^′=10. For stationary input the cortical neurons in vitro typically exhibited a more regular spiking than a Poisson process. The curves saturate for about 5–7 units of operational time.

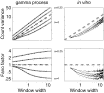Display Full Size version of this image (36K)

Fig. 5. Dependence of count statistics on observation length. (Left) The gray lines indicate the analytic solutions for the gamma process (α=0.25, 0.5, 1, 2, 4, top to bottom), the thin black lines show the corresponding simulation results. The variance of the Poisson process (gray dashed line) is equal to the expected mean count corresponding to the operational time on the abscissa Eq. (2). The Fano factor of the Poisson process is equal to 1, irrespective of the observation length T^′. For short observation intervals (T^′→0), the estimation tends to unity, irrespective of α. For large T^′, the Fano factor monotonically approaches the asymptotic value of 1/α, saturating for all gamma orders at about T^′=10. (Right) Calibration for the same five recordings as presented in Fig. 4. The count variance of the neuronal process exhibits a behavior that is very similar to the more regular point processes with gamma orders α≥2.

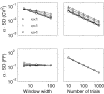Display Full Size version of this image (30K)

Fig. 6. Variance of estimation. The calibration is based on simulated ensembles of gamma processes. The standard deviation of estimating CV² (top) and FF (bottom) is approximately inversely proportional to the gamma order α. Increasing the observation length T^′ increases the average number of ISIs and, therefore, decreases the standard deviation of the CV² estimator (top left), but does not influence the reliability of the FF estimator (bottom left). With an increasing number of trials N (right panels), the standard deviation decreases as for both estimators. The estimation error is generally smaller for the CV² (top) than for the FF (bottom). In the left panels we used a fixed N=100, in the right panels we used a fixed window width T^′=100.

Display Full Size version of this image (65K)

Fig. 7. Spike time irregularity quantified in operational time. (a) Raster diagram of 20 realizations of a gamma process (α=4) simulated in operational time (left). The ISI distribution (right) is displayed in units of the mean interval μ. (b) Spike density in real time follows the deterministic rate function (gray curve). The ISI distribution (right) is broadened by the non-stationarity of rate, leading to an over-estimation of the ‘stationary’ value of CV². (c) Spike trains after de-modulation according to the empirical rate estimate (black curve in (b)). The demodulated ISIs (right) match well the gamma distribution in (a). (d) In the left panel, the estimates of CV² for true (open circles) and empirical (filled circles) operational time match well, as shown for 10 repeated simulations. By contrast, the modulated spike trains (open squares) consistently lead to a considerable over-estimation. This result is independent of the number of trials (middle panel). The positive estimation bias introduced by rate modulation is stronger for more regular processes (right).

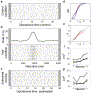Display Full Size version of this image (52K)

Fig. 8. De-modulation of spike trains. (a) Action potentials of one pyramidal neuron measured during 20 experimental control trials (stationary input condition) displayed in operational time. (b) The estimated rate function (black curve) from 20 spike trains recorded during test trials reflect the modulation of excitatory shotnoise input according to a Gaussian profile with 200 ms standard width. (c) Same spike train ensemble as in (b) after de-modulation of time using the transformation tt^′ (Eq. (2), Fig. 1). (d) Estimated cumulative distribution functions (cdf) of ISIs relative to the mean interval μ for control (blue), test (black) and de-modulated (red). (e) Q-Q plots of cumulative ISI distributions for test vs. control (black) and de-modulated vs. control (red). Colored values represent the 5%–95% inter-quantile range, gray values are outside this range. Repetition of the same experiment for 10 additional neurons for a modulation of standard width (f) 200 ms, and (g) 300 ms confirmed the good agreement of estimated CV² in the control (open circles) and de-modulated test condition (filled circles). Open squares represent the rate modulated test condition.

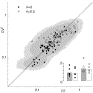Display Full Size version of this image (23K)

Fig. 9. Interval variability vs. count variability. Estimated FF and CV² from ensembles of 15 trials and for a mean spike count of 10 (see text). Recordings are from the same five neurons (different symbols) as shown in Fig. 4 and Fig. 5, for two different current stimuli with either balanced input (r_i=0.5, open symbols) or purely excitatory input (solid symbols). Dark and light gray shading represent 95% and 99% confidence regions from numerical simulations of gamma renewal processes; 108 of total 111 data points fall within the 95% region. Inset shows average values of FF (gray) and CV² (white) for both input conditions. Symbols indicate averages for individual neurons.

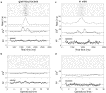Display Full Size version of this image (118K)

Fig. 10. Time resolved analysis of irregularity and variability. (a) Top panel shows 20 realizations of a rate modulated gamma process (α=2) in real time. Empirical estimates of rate function, CV² and FF are based on 100 trials, respectively. The horizontal bar indicates the analysis window of width T=385 ms. The gray horizontal line shows the asymptotic value. (b) De-modulated spike trains and time resolved measurement in operational time with a fixed window of length T^′=4. (c) Spike output of a cortical neuron during 20 repeated trials of modulated input current and time resolved measurement of CV² and FF (T=661 ms). The gray line represents the empiric values as estimated during 20 control trials (see Section 2). (d) Demodulated spike trains as in b with T^′=5.

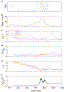Display Full Size version of this image (41K)

Fig. 11. Task-related changes of variability in monkey motor cortex. (a) Spiking activity of a motor cortical neuron during repeated trials which were aligned to the preparatory signal (PS) at time t=0. Blue circles indicate the time of movement onset. (b) Estimated firing rate shows clear task-related modulation with a strong response shortly before movement onset. (c–f) Blue curves show variability measured in original time (window width T=590 ms), red curves show variability as measured in operational time (T^′=5) after back-transformation to the experimental time axis. (c) The CV² exhibits modulations in relation to rate changes when measured on the original time axis (blue). These modulations are largely diminished when measured in operational time (red) with mean CV²=0.69 smaller than unity. (d) Measuring the CV² in each trial separately (see text) leads to a significantly reduced trial-averaged which now appears to be almost constant throughout the task with an average of 0.50 in operational time (red). (e) Task-related Fano factor is highest at the beginning of the task but strongly decreases during the period of movement preparation. At the rate response peak shortly before onset of the center-out movement the Fano factor reaches a minimum at FF≈0.5–0.6. (f) The ratio of and FF, both measured in operational time, is close to unity during the task-related rate response.

References

Aertsen et al., 1989 A.M.H.J. Aertsen, G.L. Gerstein, M.K. Habib and G. Palm, Dynamics of neuronal firing correlation: modulation of effective connectivity, J Neurophysiol 61 (1989), pp. 900–917. View Record in Scopus | Cited By in Scopus (313)

Amarasingham et al., 2006 A. Amarasingham, T.L. Chen, S. Geman, M.T. Harrison and D.L. Sheinberg, Spike count reliability and the Poisson hypothesis, J Neurosci 26 (2006), pp. 801–809. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (2)

Arieli et al., 1996 A. Arieli, A. Sterkin, A. Grinvald and A. Aertsen, Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses, Science 273 (1996), pp. 1868–1871. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (346)

Arsiero et al., 2007 M. Arsiero, H.R. Lüscher, B.N. Lundstrom and M. Giugliano, The impact of input fluctuations on the frequency–current relationships of layer 5 pyramidal neurons in the rat medial prefrontal cortex, J Neurosci 27 (2007), pp. 3274–3284. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (2)

Azouz and Gray, 1999 R. Azouz and C.M. Gray, Cellular mechanisms contributing to response variability of cortical neurons in vivo, J Neurosci 19 (1999), pp. 2209–2223. View Record in Scopus | Cited By in Scopus (133)

Baddeley et al., 1997 R. Baddeley, L.F. Abbot, Booth MCA, F. Sengpiel, T. Freeman and E.A. Wakeman, Response of neurons in primary and inferior temporal visual cortex to natural scenes, Proc R Soc Lond B 264 (1997), pp. 1775–1783. View Record in Scopus | Cited By in Scopus (111)

Badoual et al., 2005 M. Badoual, M. Rudolph, Z. Piwkowska, A. Destexhe and T. Bal, High discharge variability in neurons driven by current noise, Neurocomputing 65–66 (2005), pp. 493–498. Abstract | Full Text + Links | PDF (314 K) | View Record in Scopus | Cited By in Scopus (4)

Baker and Gerstein, 2001 S.N. Baker and G.L. Gerstein, Determination of response latency and its application to normalization of cross-correlation measures, Neural Comput 13 (2001), pp. 1351–1377. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (14)

Baker and Lemon, 2000 S.N. Baker and R. Lemon, Precise spatiotemporal repeating patterns in monkey primary and supplementary motor areas occur at chance level, J Neurophysiol 84 (2000), pp. 1770–1780. View Record in Scopus | Cited By in Scopus (49)

Barbieri et al., 2001 R. Barbieri, M.C. Quirk, L.M. Frank, M.A. Wilson and E.N. Brown, Construction and analysis of non-Poisson stimulus–response models of neural spiking activity, J Neurosci Meth 105 (2001), pp. 25–37. SummaryPlus | Full Text + Links | PDF (586 K) | View Record in Scopus | Cited By in Scopus (45)

Berry and Meister, 1998 M.J. Berry and M. Meister, Refractoriness and neural precision, J Neurosci 18 (1998), pp. 2200–2211. View Record in Scopus | Cited By in Scopus (134)

Bollimunta et al., 2007 A. Bollimunta, K.H. Knuth and M. Ding, Trial-by-trial estimation of amplitude latency variability in neuronal spike trains, J Neurosci Meth 160 (2007), pp. 163–170. SummaryPlus | Full Text + Links | PDF (670 K) | View Record in Scopus | Cited By in Scopus (0)

Boucsein et al., 2005 C. Boucsein, M.P. Nawrot, S. Rotter, A. Aertsen and D. Heck, Controlling synaptic input patterns in vitro by dynamic photo stimulation, J Neurophysiol 94 (2005), pp. 2948–2958. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (7)

Britten et al., 1993 K.H. Britten, M.N. Shadlen, W.T. Newsome and J.A. Movshon, Responses of neurons in macaque MT to stochastic motion signals, Vis Neurosci 10 (1993), pp. 1157–1169. View Record in Scopus | Cited By in Scopus (161)

Brody, 1999 C.D. Brody, Correlations without synchrony, Neural Comput 11 (1999), pp. 1537–1551. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (97)

Brown et al., 2001 E.N. Brown, R. Barbieri, V. Ventura, R.E. Kaas and L.M. Frank, The time-rescaling theorem and its application to neural spike train data analysis, Neural Comput 14 (2001), pp. 325–346.

Buracas et al., 1998 G.T. Buracas, A.M. Zador, M.R. DeWeese and T.D. Albright, Efficient discrimination of temporal patterns by motion-sensitive neurons in primate visual cortex, Neuron 20 (1998), pp. 959–969. SummaryPlus | Full Text + Links | PDF (400 K) | View Record in Scopus | Cited By in Scopus (149)

Burkitt, 2006 A.N. Burkitt, A review on the integrate-and-fire neuron model. I. Homogenous synaptic input, Biol Cybern 95 (2006), pp. 1–19. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (10)

Chacron et al., 2001 M.J. Chacron, A. Longtin and L. Maler, Negative interspike interval correlations increase the neuronal capacity for encoding time-dependent stimuli, J Neurosci 21 (2001), pp. 5328–5343. View Record in Scopus | Cited By in Scopus (65)

Chelvanayagam and Vidyasagar, 2006 D.K. Chelvanayagam and T.R. Vidyasagar, Irregularity in neocortical spike trains: influence of measurement factors and another method of estimation, J Neurosci Meth 157 (2006), pp. 264–273. SummaryPlus | Full Text + Links | PDF (512 K) | View Record in Scopus | Cited By in Scopus (0)

Churchland et al., 2006 M.M. Churchland, B.M. Yu, S.I. Ryu, G. Santhanam and K.V. Shenoy, Neural variability in premotor cortex provides a signature of motor preparation, J Neurosci 26 (2006), pp. 3697–3712. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (20)

Cox, 1962 D.R. Cox, Renewal theory. Science paperbacks., Chapman and Hall, London (1962).

Cox and Isham, 1980 D.R. Cox and V. Isham, Point processes. Monographs on applied probability and statistics., Chapman and Hall (1980).

Cox and Lewis, 1966 D.R. Cox and P.A.W. Lewis, The statistical analysis of series of events Methuen’s monographs on applied probability and statistics., Methuen, London (1966).

Davies et al., 2006 R.M. Davies, G.L. Gerstein and S.N. Baker, Measurement of time-dependent changes in the irregularity of neural spiking, J Neurophysiol 96 (2006), pp. 906–918. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (5)

Dean, 1981 A.F. Dean, The variability of discharge of simple cells in the cat striate cortex, Exp Brain Res 44 (1981), pp. 437–440. View Record in Scopus | Cited By in Scopus (96)

Dodt and Zieglgänsberger, 1990 H.U. Dodt and W. Zieglgänsberger, Visualizing unstained neurons in living brain slices by infrared dic-videomicroskopy, Brain Res 537 (1990), pp. 333–336. Abstract | PDF (494 K) | View Record in Scopus | Cited By in Scopus (120)

Fano, 1947 U. Fano, Ionization yield of radiations. II. The fluctuations of the number of ions, Phys Rev 72 (1947), pp. 26–29. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (128)

Geisler and Albrecht, 1997 W.S. Geisler and D.G. Albrecht, Visual cortex neurons in monkeys and cats: detection, discrimination, and identification, Vis Neurosci 14 (1997), pp. 897–919. View Record in Scopus | Cited By in Scopus (107)

Gestri and Petracchi, 1970 G. Gestri and D. Petracchi, The transformation induced by light stimulus on the retinal discharge: study of the interval distribution at high frequencies of sinusoidal stimulation, Kybernetik 6 (1970), pp. 171–176. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (0)

Grammont and Riehle, 2003 F. Grammont and A. Riehle, Spike synchronization and firing rate in a population of motor cortical neurons in relation to movement direction and reaction time, Biol Cybern 88 (2003), pp. 360–373. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (13)

Gur et al., 1997 M. Gur, A. Beylin and M. Snodderly, Response variability of neurons in primary visual cortex (V1) of alert monkeys, J Neurosci 17 (1997), pp. 2914–2920.

Harsch and Robinson, 2000 A. Harsch and H. Robinson, Postsynaptic variability of firing in rat cortical neurons: the roles of input synchronization and synaptic NMDA receptor conductance, J Neurosci 20 (2000), pp. 6181–6192. View Record in Scopus | Cited By in Scopus (58)

Holt et al., 1996 G.R. Holt, W.R. Softky, C. Koch and R.J. Douglas, Comparison of discharge variability in vitro and in vivo in cat visual cortex neurons, J Neurophysiol 75 (1996), pp. 1806–1814. View Record in Scopus | Cited By in Scopus (86)

Johnson, 1996 D.H. Johnson, Point process models of single-neuron discharges, J Comput Neurosci 3 (1996), pp. 275–299. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (60)

Kara et al., 2000 P. Kara, P. Reinagel and C. Reid, Low response variability in simultaneously recorded retinal, thalamic, and cortical neurons, Neuron 27 (2000), pp. 635–646. SummaryPlus | Full Text + Links | PDF (459 K) | View Record in Scopus | Cited By in Scopus (81)

Kargo and Nitz, 2004 W.J. Kargo and D.A. Nitz, Improvements in the signal-to-noise ratio of motor cortex cells distinguish early versus late phases of motor skill learning, J Neurosci 24 (2004), pp. 5560–5569. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (11)

Kass and Ventura, 2001 R.E. Kass and V. Ventura, A spike-train probability model, Neural Comput 13 (2001), pp. 1713–1720. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (30)

Kisley and Gerstein, 1999 M. Kisley and G. Gerstein, Trial-to-trial variability and state-dependent modulation of auditory-evoked responses in cortex, J Neurosci 23 (1999), pp. 10451–10460. View Record in Scopus | Cited By in Scopus (46)

Knoblauch and Palm, 2005 A. Knoblauch and G. Palm, What is signal and what is noise in the brain?, BioSystems 79 (2005), pp. 83–90. Abstract | Full Text + Links | PDF (225 K) | View Record in Scopus | Cited By in Scopus (5)

Lee et al., 1998 D. Lee, N.L. Port, W. Kruse and A.P. Georgopoulos, Variability and correlated noise in the discharge of neurons in motor and parietal areas of the primate cortex, J Neurosci 18 (1998), pp. 1161–1170. View Record in Scopus | Cited By in Scopus (110)

Lindner, 2004 B. Lindner, Interspike interval statistics of neurons driven by colored noise, Phys Rev E 69 (2004), pp. 0229011–0229014.

Masuda and Aihara, 2003 N. Masuda and K. Aihara, Ergodicity of spike trains: when does trial averaging make sense?, Neural Comput 15 (2003), pp. 1341–1372. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (7)

Maynard et al., 1999 E.M. Maynard, N.G. Hatsopoulos, C.L. Ojakangas, B.D. Acuna, J.N. Sanes and R.A. Normann, Neuronal interactions improve cortical population coding of movement direction, J Neurosci 19 (1999), pp. 8083–8093. View Record in Scopus | Cited By in Scopus (101)

Mazurek and Shadlen, 2002 M.E. Mazurek and M.N. Shadlen, Limits to the temporal fidelity of cortical spike rate signals, Nat Neurosci 5 (2002), pp. 463–471. View Record in Scopus | Cited By in Scopus (39)

Meier et al., 2007 R. Meier, S. Gruen, C. Boucsein, A. Aertsen, K.H. Boven and U. Egert, Characterizing neural network dynamics: analyzing neural activity data using the FIND-toolbox. No. 319.11. 2007, Neuroscience Meeting Planner, Society for Neuroscience, San Diego, CA (2007) Online.

Murthy and Fetz, 1996 V.N. Murthy and E. Fetz, Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys, J Neurophysiol 76 (1996), pp. 3968–3982. View Record in Scopus | Cited By in Scopus (163)

Nawrot, 2003 Nawrot MP. Ongoing activity in cortical networks: noise, variability and context. PhD thesis. Faculty of Biology, Albert-Ludwigs-University Freiburg, Germany; 2003.

Nawrot et al., 1999 M.P. Nawrot, A. Aertsen and S. Rotter, Single-trial estimation of neuronal firing rates: from single-neuron spike trains to population activity, J Neurosci Meth 94 (1999), pp. 81–92. SummaryPlus | Full Text + Links | PDF (489 K) | View Record in Scopus | Cited By in Scopus (22)

Nawrot et al., 2003a M.P. Nawrot, A. Aertsen and S. Rotter, Elimination of response latency variability in neuronal spike trains, Biol Cybern 88 (2003), pp. 321–334. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (9)

Nawrot et al., 2007 Nawrot MP, Boucsein C, Rodriguez-Molina V, Aertsen A, Grün S, Rotter S. Serial interval statistics of spontaneous activity in cortical neurons in vivo and in vitro. Neurocomputing 2007;70:1717–22.

Nawrot et al., 2003b M.P. Nawrot, T. Pistohl, S. Schrader, U. Hehl, V. Rodriguez and A. Aertsen, Embedding living neurons into simulated neural networks., Proceedings of the 1st international IEEE EMBS conference on neural engineering Capri Island (Italy) (2003), pp. 229–232.

Nawrot et al., 2001 M.P. Nawrot, V. Rodriguez, D. Heck, A. Riehle, A. Aertsen and S. Rotter, Trial-by-trial variability of spike trains in vivo and in vitro, Soc Neurosci Abstr 27 (2001), p. 64.9.

Nowak et al., 1997 L.G. Nowak, M.V. Sanchez-Vives and D.A. McCormick, Influence of low and high frequency inputs on spike timing in visual cortical neurons, Cereb Cortex 7 (1997), pp. 487–501. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (129)

Oata, 1988 Y. Oata, Statistical models for earthquake occurrences and residual analysis for point processes, J Am Statist Assoc 83 (1988), pp. 9–27.

Oram et al., 2001 M.W. Oram, N.G. Hatsopoulos, B.J. Richmond and J.P. Donoghue, Excess synchrony in motor cortical neurons provides redundant direction information with that from coarse temporal measures, J Neurophysiol 86 (2001), pp. 1700–1716. View Record in Scopus | Cited By in Scopus (37)

Oram et al., 1999 M.W. Oram, M.C. Wiener, R. Lestienne and B.J. Richmond, Stochastic nature of precisely timed spike patterns in visual system neuronal responses, J Neurophysiol 81 (1999), pp. 3021–3033. View Record in Scopus | Cited By in Scopus (81)

Parzen, 1962 E. Parzen, On estimation of a probability density function and mode, Ann Math Stat 33 (1962), pp. 1065–1076. MathSciNet

Paulin and Hoffman, 2001 M.G. Paulin and L.F. Hoffman, Optimal firing rate estimation, Neural Networks 14 (2001), pp. 877–881. SummaryPlus | Full Text + Links | PDF (94 K) | View Record in Scopus | Cited By in Scopus (10)

Pauluis and Baker, 2000 Q. Pauluis and S.N. Baker, An accurate measure of the instantaneous discharge probability, with application to unitary joint-event analysis, Neural Comput 12 (2000), pp. 647–669. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (25)

Perkel et al., 1967a D.H. Perkel, G.L. Gerstein and G.P. Moore, Neuronal spike trains and stochastic point processes. I. The single spike train, Biophys J 7 (1967), pp. 391–418. View Record in Scopus | Cited By in Scopus (162)

Perkel et al., 1967b D.H. Perkel, G.L. Gerstein and G.P. Moore, Neuronal spike trains and stochastic point processes. II. Simultaneous spike trains, Biophys J 7 (1967), pp. 419–440. View Record in Scopus | Cited By in Scopus (346)

Prut and Perlmutter, 2003 I. Prut and S.I. Perlmutter, Firing properties of spinal interneurons during voluntary movement. I. State-dependent regularity of firing, J Neurosci 29 (2003), pp. 9600–9610.

Ratnam and Nelson, 2000 R. Ratnam and M.E. Nelson, Nonrenewal statistics of electrosensory afferent spike trains: implications for the detection of weak sensory signals, J Neurosci 20 (2000), pp. 6672–6683. View Record in Scopus | Cited By in Scopus (41)

Reich et al., 1998 D.S. Reich, J.D. Victor and B.W. Knight, The power ratio and the interval map: spiking models and extracellular recordings, J Neurosci 18 (1998), pp. 10090–10104. View Record in Scopus | Cited By in Scopus (41)

Ripley, 1987 B.D. Ripley, Stochastic simulation Wiley series in probability and mathematical statistics, John Wiley & Sons, New York (1987).

Rotter et al., 2005 S. Rotter, A. Riehle, V. Rodriguez-Molina, A. Aertsen and M.P. Nawrot, Different time scales of spike train variability in motor cortex. Program No. 276.7. 2005, Abstract Viewer/Itinerary Planner, Society for Neuroscience, Washington, DC (2005) Online.

Shadlen and Newsome, 1998 M.N. Shadlen and W.T. Newsome, The variable discharge of cortical neurons: implications for connectivity, computation, and information coding, J Neurosci 18 (1998), pp. 3870–3896. View Record in Scopus | Cited By in Scopus (487)

Snowden et al., 1992 R. Snowden, S. Treue and R. Anderson, The response of neurons in areas V1 and MT of the alert rhesus monkey to moving random dot patterns., Exp Brain Res 88 (1992), pp. 389–400. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (98)

Softky and Koch, 1993 W.R. Softky and C. Koch, The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs, J Neurosci 13 (1993), pp. 334–350. View Record in Scopus | Cited By in Scopus (495)

Stein, 1965 R.B. Stein, A theoretical analysis of neuronal variability, Biophys J 5 (1965), pp. 173–194.

Stein et al., 2005 R.B. Stein, E.R. Gossen and K.E. Jones, Neuronal variability: noise or part of the signal?, Nat Rev Neurosci 6 (2005), pp. 389–397. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (27)

Stevens and Zador, 1998 C.F. Stevens and A.M. Zador, Input synchrony and the irregular firing of cortical neurons, Nat Neurosci 1 (1998), pp. 210–217. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (159)

Teich et al., 1997 M.C. Teich, C. Heneghan, S.B. Lowen, T. Ozaki and E. Kaplan, Fractal character of the neural spike train in the visual system of the cat, J Opt Soc Am A 14 (1997), pp. 529–546. View Record in Scopus | Cited By in Scopus (65)

Teich et al., 1996 M.C. Teich, R.G. Turcott and R.M. Siegel, Temporal correlation in cat striate-cortex neural spike trains, IEEE Eng Med Biol Mag 15 (1996), pp. 79–87. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (27)

Truccolo et al., 2005 W. Truccolo, U.T. Eden, M.R. Fellows, J.P. Donoghue and E.N. Brown, A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects, J Neurophysiol 93 (2005), pp. 1074–1089. View Record in Scopus | Cited By in Scopus (25)

Tuckwell, 1988 H.C. Tuckwell, Introduction to theoretical neurobiology, vol. 2, Cambridge University Press, Cambridge (1988).

Ventura, 2004 V. Ventura, Testing for and estimating latency effects for poisson and non-poisson spike trains, Neural Comput 16 (2004), pp. 2323–2349. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (4)

Ventura et al., 2005 V. Ventura, C. Cai and R.E. Kass, Trial-to-trial variability and its effect on time-varying dependency between two neurons, J Neurophysiol 94 (2005), pp. 2928–2939. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (8)

Vogels and Orban, 1991 R. Vogels and G. Orban, Quantitative study of striate single unit responses in monkeys performing an orientation discrimination task, Exp Brain Res 84 (1991), pp. 1–11. View Record in Scopus | Cited By in Scopus (27)

Vogels et al., 1989 R. Vogels, W. Spileers and G. Orban, The response variability of striate cortical neurons in the behaving monkey, Exp Brain Res 77 (1989), pp. 432–436. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (88)

Wiener, 2003 M.C. Wiener, An adjustment of the time-rescaling method for application to short-trial spike train data, Neural Comput 15 (2003), pp. 2565–2576. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (0)