
Science,
Vol 278,
Issue 5345,
1901-1902
, 12 December 1997
[DOI: 10.1126/science.278.5345.1901]
NEUROSCIENCE:
Temporal Coding in Neural Populations?
Eberhard E. Fetz
The waking brain continually performs a remarkable
range of neural computations, processing its interactions with the
environment as well as performing numerous internal operations.
Consider the immediate example of your ability to quickly comprehend
the spatial patterns on this page. Scanning successive words and
decoding their meaning is a common miracle performed effortlessly by
cerebral networks. If you pause to contemplate how neurons could
perform these feats, your thoughts are also generated by a complex
calculus of neural impulses. Realizing that your entire mental
existence depends on neural operations, you can appreciate why
neuroscientists would like to understand the underlying mechanisms.
To investigate how neurons process information, researchers typically
relate the firing rate of single neurons (the rate at which neurons
generate all-or-none action potentials) to a behavioral parameter, such
as a sensory stimulus or motor response (1-3).
Neural activity is quite variable, even with precise repetitions of the
behavioral conditions, so mean firing rates have been obtained by
averaging neural responses over many trials, thereby enhancing the
rate-coding "signal." The success of this approach has led to the
belief that firing rates of neurons are the necessary and sufficient
mechanism underlying information processing, and furthermore, that
firing rates not only code peripheral sensory and motor events, but
also mediate central cognitive processes.
But in fact, large populations of neurons are involved simultaneously in any behavior (4),
and the temporal structure of spike activity in neural assemblies
provides additional dimensions for coding information. Increasing
numbers of researchers are now recording from many neurons
simultaneously (3, 4). Indeed,
the techniques for multiunit recording have outstripped the development
of algorithms for analyzing the dynamics of neural populations. Some
investigators have found ways to derive better fits between multiunit
activity and behavioral parameters (3), but most
population-coding schemes still employ functions of firing rates. The
possibility that information processing may involve the instantaneous
relations between members of neural assemblies has been proposed (5, 6), although such ideas are in dire need of compelling experimental support. In this regard, the report on page 1950 of this issue by Riehle et al. (7)
provides new tools and supporting evidence. Using a simple algorithm
for detecting real-time interactions in neural populations, the authors
have found that neural activity became transiently synchronized during
a purely internal cognitive process--when a monkey expected the
presentation of a signal, in the absence of any sensory or motor events.
These findings relate to a current controversy concerning neural
coding: whether neurons process information only by rate coding or
whether the brain also exploits "temporal coding," in which the
relative timing of spikes can carry information (1, 7-10, 14). Temporal coding can employ the temporal structure of the firing pattern of single neurons (10) or, as considered here, the precise relation between firings in multiple neurons of a functional assembly (5, 9, 12, 14).
If the relative timing of spikes in a neural population can represent
information, as it surely does in the auditory system, the "bandwidth"
for neural processing could be significantly expanded. As yet, there is
no accepted standard for how this increased channel capacity would be
used for high-definition neural computation. But a common feature of
most temporal codes is the synchronization of spikes in neurons. The
report by Riehle et al. shows that motor cortex neurons can
become significantly more synchronized in relation to expected events,
independently of any changes in firing rates.
The figure illustrates the different types of neural interactions. The
two representative neurons (A and B) can fire in relation to peripheral
events, like a sensory stimulus (S) or movement (M), and can also
participate in internal cognitive events, symbolized by the central
assembly (C). The proposed signature of the cells' participation in
assembly activity is increased synchronization, produced by common
input from the assembly. Synchronous activity provides an effective
propagating mechanism within the assembly, and can also change the
efficacy of synaptic connections between the synchronized cells (9). Riehle et al.
detected the increased synchrony by comparing the number of observed
coincident spikes (red bars) with the number expected by chance, based
on a running estimate of rates over a longer interval (blue bar). This
running comparison can identify exceptional synchronizations whenever
they occur. Interestingly, these occurred at times when the monkey
expected a possible cue, as well as when he made a motor response.
Thus, synchronization and rate coding can occur separately or together (8, 9, 12, 14, 15).
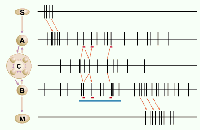
Neural communication. Schematic representation of
interactions of two cortical neurons (A and B). Sensory event S affects
A and motor output M is affected by B; in both cases the neuronal
firing rate codes a peripheral parameter. The central assembly (C) can
also engage A and B in synchronous activity. This can be detected by
the increased synchrony in the brief intervals (red) compared to that
expected from activity in the longer interval (blue).
Several other approaches can detect coherent activity in neural
populations at millisecond resolution. Standard cross-correlations
between simultaneously recorded neurons commonly reveal synchronous
activity, and time-dependent cross-correlation measures (11) have revealed that synchronous firing can be rapidly modulated with behavior, even without changes in firing rates (12). Other studies have found evidence for precisely timed patterns occurring among neural groups in a behavioral situation (5). Simulations have shown that such synchrony can be preserved in chains of neurons with realistic synaptic connections (13).
Another form of synchronized activity in neural populations is the
widespread periodic oscillations seen in visual cortex neurons, which
has been suggested to subserve a binding function (9), a suggestion potentially applicable to coordination of motor responses (14, 15). Another approach uses the "gravity" method to identify groups of neurons that tend to fire in synchrony: If n neurons are located in n-dimensional
space, and their spikes are endowed with a transient "charge," those
cells that fire synchronously tend to be attracted and form
identifiable clusters (6).
Although all of these algorithms can detect the existence of precise
temporal structure in neural activity, this does not yet establish
their function as a temporal code. What is needed first is some
demonstration that synchronization occurs reliably under particular
behavioral conditions. The accumulating evidence is suggestive (5-9, 12, 14)
but still leaves the exact function unproven. Establishing the
functional mechanism may not be a matter of finding tighter
correlations with behavioral events; for example, holographic
mechanisms code distributed information in terms of phase relations
rather than literal representations (2). Skeptics
can still argue that the temporal events revealed by these methods are
epiphenomena or products of the statistical models, and that anything
temporal coding can do, population rate coding can do as well (16). Moreover, there are open questions about how temporal codes are established and how they interact with rate coding (8, 15).
These issues can now be investigated with the tools at hand: Multiunit
recordings can be analyzed with these algorithms, and the detected
events can be related to behavior. Neural network simulations can also
help to demonstrate how the putative coding mechanisms could actually
work (2, 5, 13). This combination of approaches should crack the temporal code one way or the other.
References
- F. Riecke, D. Warland, R. van Steveninck, W. Bialek, Spikes (MIT Press, Cambridge, MA, 1997).
- E. Fetz, Behav. Brain Sci. 15, 679 (1992).
- A. P. Georgopoulos et al., J. Neurosci. 8, 2928 (1988) [Medline]; M. Taira et al., Exp. Brain Res. 109, 367 (1996) [Medline]; E. Salinas and L. Abbott, J. Comp. Neurosci. 1, 89 (1994); K. Zhang, I. Ginzburg, B. L. McNaughton, T. J. Sejnowski, J. Neurophysiol., in press.
- C. Koch and J. L. Davis, Large-Scale Neuronal Theories of the Brain (MIT Press, Cambridge, MA, 1994).
- M. Abeles et al., J. Neurophysiol. 70, 1629 (1993) [Medline]; M. Abeles, Corticonics (Cambridge Univ. Press, Cambridge, 1991); M. Abeles et al., in Brain Theory: Spatio-temporal Aspects of Brain Function, A. Aertsen, Ed. (Elsevier, Amsterdam, 1993), pp. 149-181.
- G. Gerstein, and A. Aertsen, J. Neurophysiol. 54, 1513 (1985) [Medline]; G. Gerstein, D. H. Perkel, J. E. Dayhoff, J. Neurosci. 5, 881 (1985) [Medline]; B. G. Lindsey et al., J. Neurophysiol. 78, 1714 (1997) [Medline].
- A. Riehle, S. Grün, M. Diesmann, A. Aertsen, Science 278, 1950.
- G. Buszaki, R. Llinas, W. Singer, A. Berthoz, Y. Christen, Eds., Temporal Coding in the Brain (Springer-Verlag, New York, 1994).
- W. Singer, Annu. Rev. Physiol. 55, 349 (1993) [Medline]; in (4), pp. 201-237.
- D. Ferster and N. Spruston, Science 270, 756 (1995).
- A. Aertsen, G. L. Gerstein, M. K. Habib, G. Palm, J. Neurophysiol. 61, 900 (1989) [Medline].
- E. Vaadia et al., Nature 373, 515 (1995) [Medline].
- A. Aertsen, M. Diesmann, M.-O. Gewaltig, J. Physiol. (Paris) 90, 243 (1996).
- P. R. Roelfsema, A. K. Engel, P. König, W. Singer, J. Cogn. Neurosci. 8, 603 (1996).
- V. N. Murthy and E. Fetz, J. Neurophysiol. 76, 3968 (1996) [Medline].
- M. Shadlen and W. T. Newsome, Curr. Opin. Neurobiol. 4, 569 (1994); J. N. Sanes and J. P. Donoghue, Proc. Natl. Acad. Sci. U.S.A. 90, 4470 (1993) [Medline].
The author is in the Department of Physiology and Biophysics, University of Washington, Seattle, WA 98195-7290, USA. E-mail: Fetz@u.washington.edu
This article has been cited by other articles:
- Hurtado, J. M., Rubchinsky, L. L., Sigvardt, K. A.
(2004). Statistical Method for Detection of Phase-Locking Episodes in Neural Oscillations. J. Neurophysiol.
91: 1883-1898
[Abstract]
[Full Text]
- Morris, K. F., Baekey, D. M., Nuding, S. C., Dick, T. E., Shannon, R., Lindsey, B. G.
(2003). Plasticity in Respiratory Motor Control: Invited Review: Neural network plasticity in respiratory control. J. Appl. Physiol.
94: 1242-1252
[Abstract]
[Full Text]
- Grun, S., Diesmann, M., Aertsen, A.
(2002). Unitary Events in Multiple Single-Neuron Spiking Activity: I. Detection and Significance. Neural Comput
14: 43-80
[Abstract]
[Full Text]
- Chang,
E. Y., Morris, K. F., Shannon, R., Lindsey, B. G. (2000). Repeated
Sequences of Interspike Intervals in Baroresponsive Respiratory Related
Neuronal Assemblies of the Cat Brain Stem. J. Neurophysiol.
84: 1136-1148
[Abstract]
[Full Text]
- Pauluis, Q., Baker, S. N.
(2000). An Accurate Measure of the Instantaneous Discharge Probability, with Application to Unitary Joint-Event Analysis. Neural Comput
12: 647-669
[Abstract]
[Full Text]
- Chang, H.-S., Staras, K., Gilbey, M. P.
(2000). Multiple Oscillators Provide Metastability in Rhythm Generation. J. Neurosci.
20: 5135-5143
[Abstract]
[Full Text]
- Arata, A., Hernandez, Y. M., Lindsey, B. G., Morris, K. F., Shannon, R.
(2000). Transient configurations of baroresponsive respiratory-related brainstem neuronal assemblies in the cat. J Physiol
525: 509-530
[Abstract]
[Full Text]
- Goodwin,
A. W., Wheat, H. E. (1999). Effects of Nonuniform Fiber Sensitivity,
Innervation Geometry, and Noise on Information Relayed by a Population
of Slowly Adapting Type I Primary Afferents from the Fingerpad. J. Neurosci.
19: 8057-8070
[Abstract]
[Full Text]
- Chang, H.-S., Staras, K., Smith, J. E., Gilbey, M. P.
(1999). Sympathetic Neuronal Oscillators are Capable of Dynamic Synchronization. J. Neurosci.
19: 3183-3197
[Abstract]
[Full Text]
Volume 278,
Number 5345,
Issue of 12 Dec 1997,
pp. 1901-1902.
Copyright © 1997 by The American Association for the Advancement of Science. All rights reserved.
|

